由沃·兹基·边德研究所最新的研究报告表明，
点在提升玩家智力水平的同时，更有助于提升玩家的颜值。所以即日起，我们向广大用户提供
点颜值大礼包。
礼包一：


礼包二：


礼包三：


这个经理为何如此面熟？快来这里看看吧！


我们向您承诺：介绝对四里没有挽过的船新版本，挤需体验三番钟，里造会干我一样，爱象节款游戏。还等什么？快来学习算法领取大礼包吧！


21点玩法简介


确定策略！


假设有无数副扑克牌用于游戏。如此，就可以认为从牌堆中新获取的牌与弃牌堆牌的点数无关。且庄家的策略是固定的：已有的点数和小于
点则拿牌，反之，大于等于
点则停牌。在这里为简化情况，我们只比较拿牌和停牌两种策略，而不考虑分牌，保险真人视频游戏，双倍下注等策略。
庄家篇：


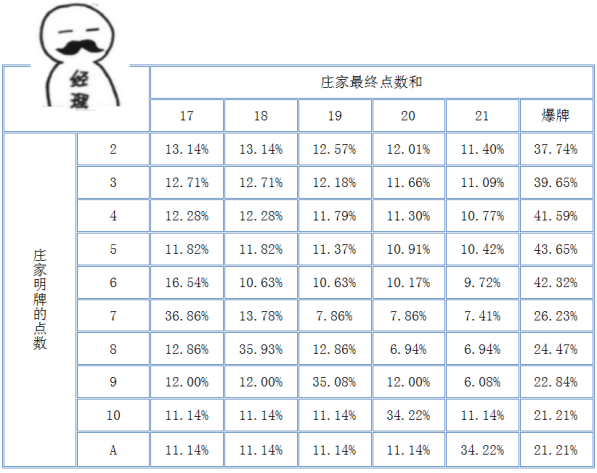
我们首先分析庄家的策略，假设游戏开始时，庄家明牌的点数为
。


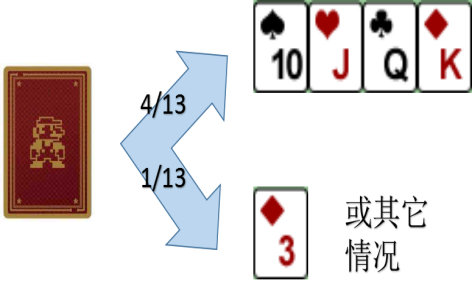
那么庄家两张牌的点数和为
的概率（即暗牌为
）是
。同理，为可能的其他点数和（例如点数和为
，即暗牌点数为
）的概率为
。


以此类推，我们可以得到下面这张概率表：


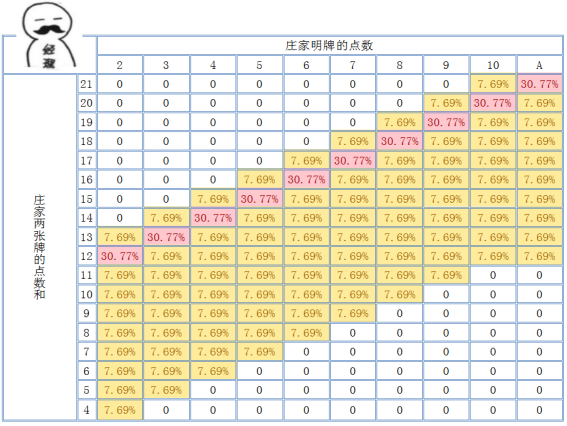
有兴趣的同学可以自行验证最后一列，明牌为
的情况。这样，结合一开始提出的庄家固定策略，我们还可以得到庄家已有点数和与最终点数和的关系。


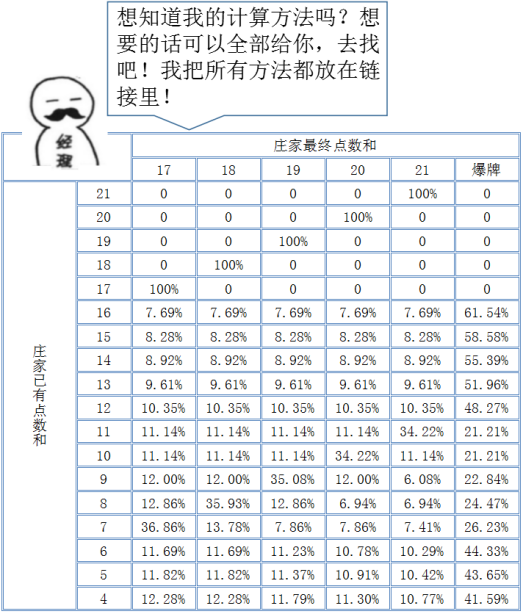
状态转移矩阵


现在我们由庄家明牌的点数确定了庄家已有点数和的概率，进而确定了庄家最终点数和的概率。这个时候，将上述两个矩阵转置相乘，我们就可以得到庄家明牌的点数和最终点数和的关系了。


玩家篇：
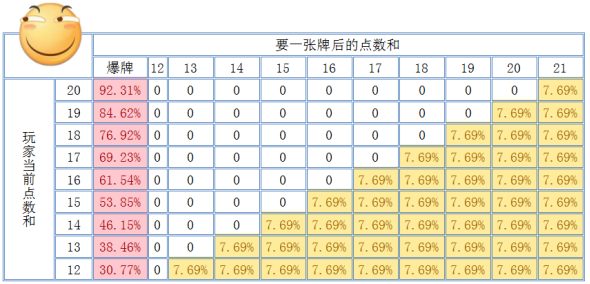
以上是有关庄家的情况，下面我们来观察一下玩家的策略。显然的是，当玩家已有点数和小于
时，拿牌一定是最佳策略。而当已有点数等于
时，停牌一定是最佳策略。所以我们只考虑已有点数介于
与
（含端点）的情况。同样的，我们可以得到玩家要一张牌后，点数和对应的概率。


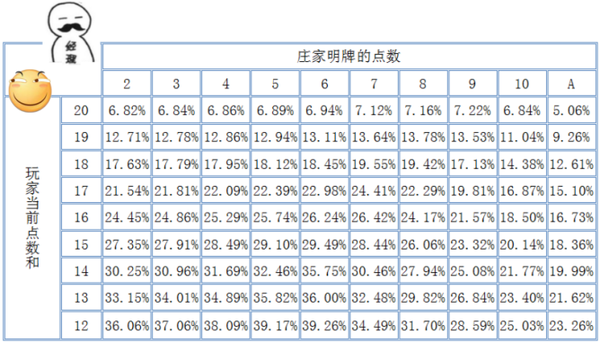
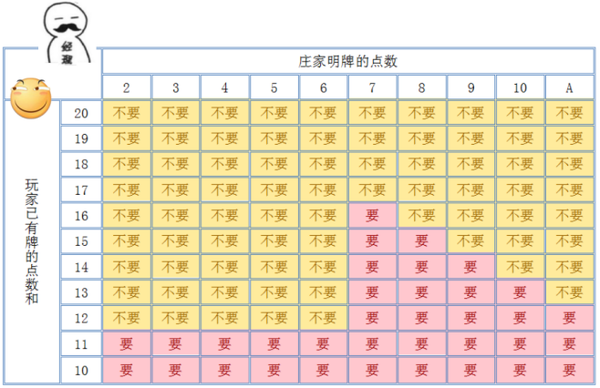
结合玩家的胜利条件：
1. 双方都没有爆牌的情况下，玩家最终点数和大于庄家。
2. 玩家没有爆牌的情况下，庄家爆牌。
以及庄家篇最后得到的结论，列出玩家在不同情况下，选择要一张牌的胜率表：


以及选择不要牌的胜率表：


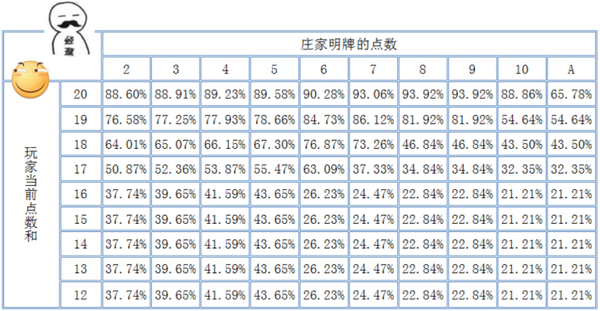
对比两张胜率表，我们就能很容易的确定我们的策略了。


制定规则！
下面我们简化规则，制定一个简单的游戏流程来测试一下我们的策略：


第
阶段：无限牌堆加入游戏。玩家策略加入游戏。庄家固定策略加入游戏。 判定庄家和玩家手牌是否为黑杰克，若两方皆为黑杰克，则判定平局，该轮游戏结束。若只有其中一方为黑杰克，则判定拥有黑杰克的一方获胜，该轮游戏结束。若双方都没有黑杰克，则进入第
阶段。
第
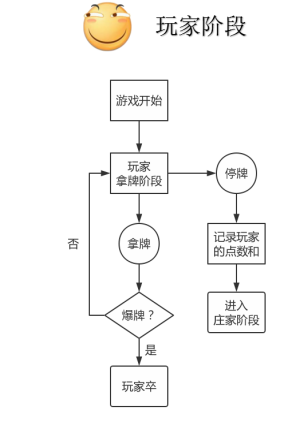
阶段：玩家加入游戏。
游戏开始时，先进入玩家阶段，由玩家决定是否拿牌。若玩家在一次或多次拿牌后爆牌则判定庄家胜，该轮游戏结束。若不然，玩家可以随时停牌，此时记录玩家当前点数和，进入第
阶段。


第
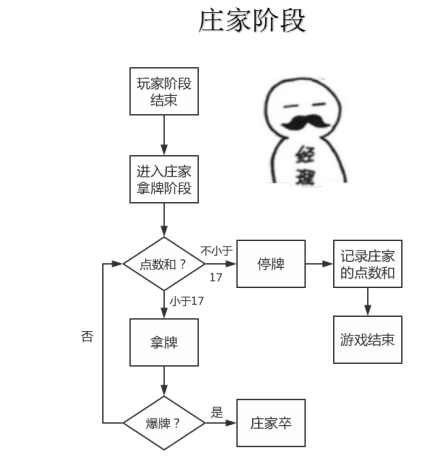
阶段：
玩家阶段结束后，进入庄家阶段。庄家采用固定策略,当前点数和小于
则拿牌，反之则停牌。同样的，若庄家在一次或多次拿牌后爆牌则判定玩家胜，该轮游戏结束。若不然，庄家直到当前点数和大于或等于
时停牌，此时记录庄家当前点数和，进入第
阶段。


第
阶段：裁判加入游戏。
判断庄家和玩家最终点数和的大小关系，若玩家的最终点数和较大，则判定玩家获胜，其他情况判定为庄家获胜。该轮游戏结束，进入下一轮游戏。
测试阶段！
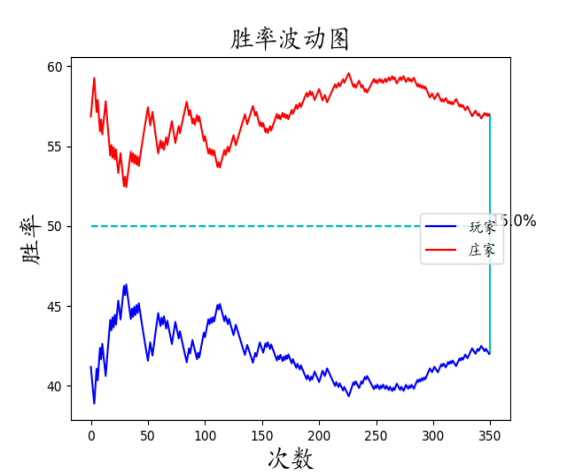
我们模拟了
次策略实施的情况，并统计庄家和玩家的实时胜率，从第
次开始，我们用红线表示庄家的实时胜率变化，蓝线表示玩家的实时胜率变化，我们得到的绝大部分（造数君估计在
%以上）是下面两种类型的图：
泯然众图型：

输少算赢型：

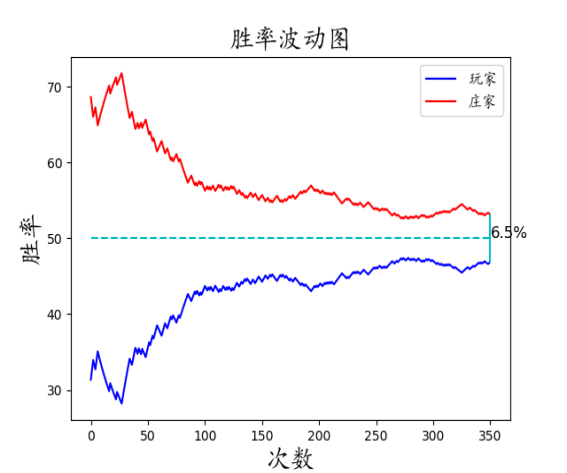
可以看到大部分的图，红线与蓝线是没有交点的，即玩家被庄家完全碾压。当然由于我们只是从第
次开始计数，所以也有比较反常的现象：
中期强势型：

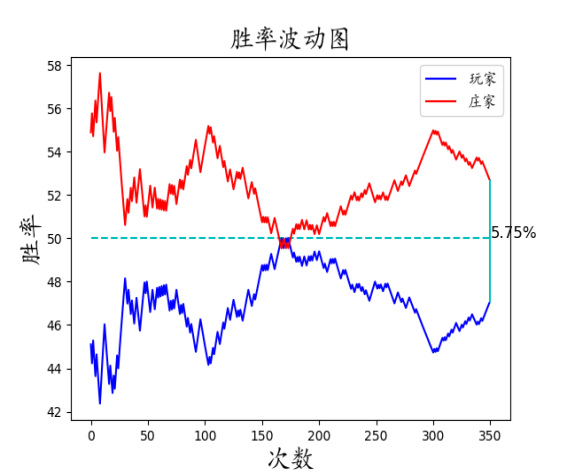
后期疲软型：

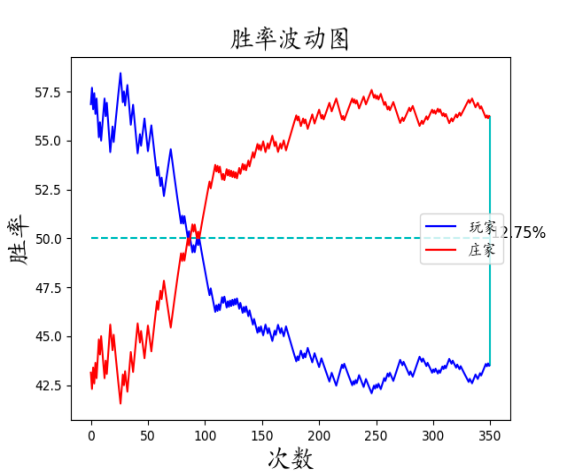
同时也出现了医学上难以解释的现象：
回光返照型：

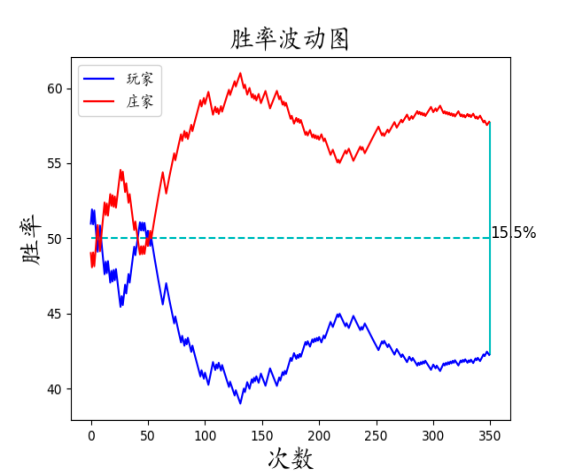
以及它的变种：
大起大落型：

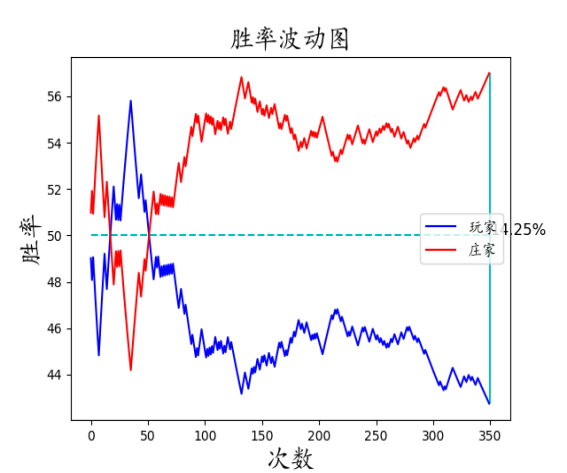
以及变种的变种：
起起落落落落落落落落落落落落型：

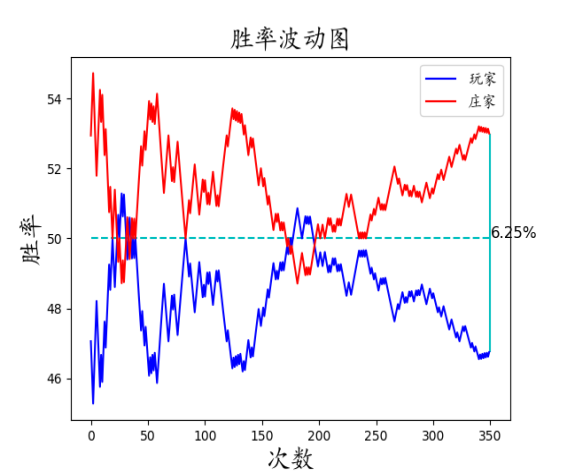
可以看到在无限牌堆，模拟次数足够多的情况下，玩家都难逃被庄家压制的情况。不论其间有多少次胜率上升的情况，最后都会落落落落落到低点。


也许这就是人生吧。


彩蛋！
有兴趣的小伙伴可以私信造数君领取：模拟玩家策略在有限牌堆和无限牌堆的胜率变化代码哦~