你想玩这个不是不可以，关键是得懂一些技术，不懂技术其实就完全是等于在白白的把钱扔给别人


任何一款游戏都会存在漏洞，就像人一样，世界上不会有完美无缺的人，也不会存在完美无缺的游戏。
其实无非就是读取本地内存数据，实现透视效果视讯直播，这个是被加密存放的，里边存放着各种牌的数据，可以通过读取本地加密数据实现，但如果要改变牌大小，这个得逆向渗透，相对麻烦复杂一些。
通过技术手段，在游戏里得到明文发包函数，这个对我们逆向用处不小，可以去进行HOOK，然后就分析封包，HOOK明文包进行分析是必然的，因为直接在OD软件中下断分析会比较男难，动作也会比较频繁，所以HOOK明文函数就相当于直接省去了解密过程。








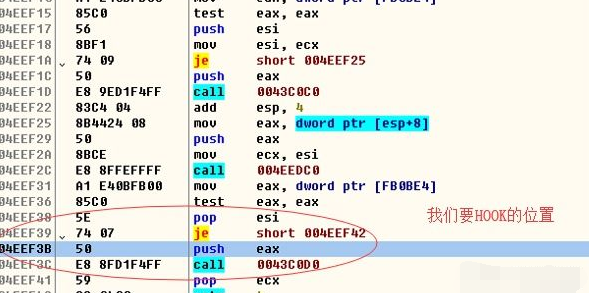
在此明文法宝CALL上HOOK这几个字节即可，然后将其修改成JMP xxxx 跳转到我们自己DLL的子程序里，执行我们想执行的过程，然后再跳转出去，
需要注意的是，此过程不能对游戏代码产生任何影响，包括寄存器的值和堆栈。
由于隐私问题再这里只放出了一小部分代码，
下面我们来看看成果如何






先开启游戏，然后打开辅助工具，进行数据拦截，










这样一来接下来什么牌我们都可以提前得知了，
当然这只是个人的一个小测试，只是给大家来讲解分析一下这个事的原理
所以说，你不懂技术，还是不要碰这个东西的好
有需要的参考下图找我交流








































































import numpy as np


""" Here I implemented the scoring functions.
MAE, MSE, RMSE, RMSLE are included.
Those are used for calculating differences between
predicted values and actual values.
Metrics are slightly differentiated. Sometimes squared, rooted,
even log is used.
Using log and roots can be perceived as tools for penalizing big
errors. However, using appropriate metrics depends on the situations,
and types of data
"""


# Mean Absolute Error
def mae(predict, actual):
"""
Examples(rounded for precision):
>>> actual = [1,2,3];predict = [1,4,3]
>>> np.around(mae(predict,actual),decimals = 2)
0.67
>>> actual = [1,1,1];predict = [1,1,1]
>>> mae(predict,actual)
0.0
"""
predict = np.array(predict)
actual = np.array(actual)


difference = abs(predict - actual)
score = difference.mean()


return score




# Mean Squared Error
def mse(predict, actual):
"""
Examples(rounded for precision):
>>> actual = [1,2,3];predict = [1,4,3]
>>> np.around(mse(predict,actual),decimals = 2)
1.33
>>> actual = [1,1,1];predict = [1,1,1]
>>> mse(predict,actual)
0.0
"""
predict = np.array(predict)
actual = np.array(actual)


difference = predict - actual
square_diff = np.square(difference)


score = square_diff.mean()
return score




# Root Mean Squared Error
def rmse(predict, actual):
"""
Examples(rounded for precision):
>>> actual = [1,2,3];predict = [1,4,3]
>>> np.around(rmse(predict,actual),decimals = 2)
1.15
>>> actual = [1,1,1];predict = [1,1,1]
>>> rmse(predict,actual)
0.0
"""
predict = np.array(predict)
actual = np.array(actual)


difference = predict - actual
square_diff = np.square(difference)
mean_square_diff = square_diff.mean()
score = np.sqrt(mean_square_diff)
return score




# Root Mean Square Logarithmic Error
def rmsle(predict, actual):
"""
Examples(rounded for precision):
>>> actual = [10,10,30];predict = [10,2,30]
>>> np.around(rmsle(predict,actual),decimals = 2)
0.75
>>> actual = [1,1,1];predict = [1,1,1]
>>> rmsle(predict,actual)
0.0
"""
predict = np.array(predict)
actual = np.array(actual)


log_predict = np.log(predict + 1)
log_actual = np.log(actual + 1)


difference = log_predict - log_actual
square_diff = np.square(difference)
mean_square_diff = square_diff.mean()


score = np.sqrt(mean_square_diff)


return score




# Mean Bias Deviation
def mbd(predict, actual):
"""
This value is Negative, if the model underpredicts,
positive, if it overpredicts.
Example(rounded for precision):
Here the model overpredicts
>>> actual = [1,2,3];predict = [2,3,4]
>>> np.around(mbd(predict,actual),decimals = 2)
50.0
Here the model underpredicts
>>> actual = [1,2,3];predict = [0,1,1]
>>> np.around(mbd(predict,actual),decimals = 2)
-66.67
"""
predict = np.array(predict)
actual = np.array(actual)


difference = predict - actual
numerator = np.sum(difference) / len(predict)
denumerator = np.sum(actual) / len(predict)
# print(numerator, denumerator)
score = float(numerator) / denumerator * 100


return score